Iterative Most Likely Oriented Point Registration (IMLOP)

The iterative closest point (ICP) algorithm is a popular method for registering geometric representations of 3D shapes and has been extensively applied to problems of rigid body shape alignment in medical research. Many variants of ICP have been introduced. All ICP-based algorithms seek optimal alignment by iterating two key algorithmic steps: a correspondence phase that computes a match on the target shape for each point comprising the source shape and a registration phase that computes the rigid body transformation that optimally aligns the matched point pairs.

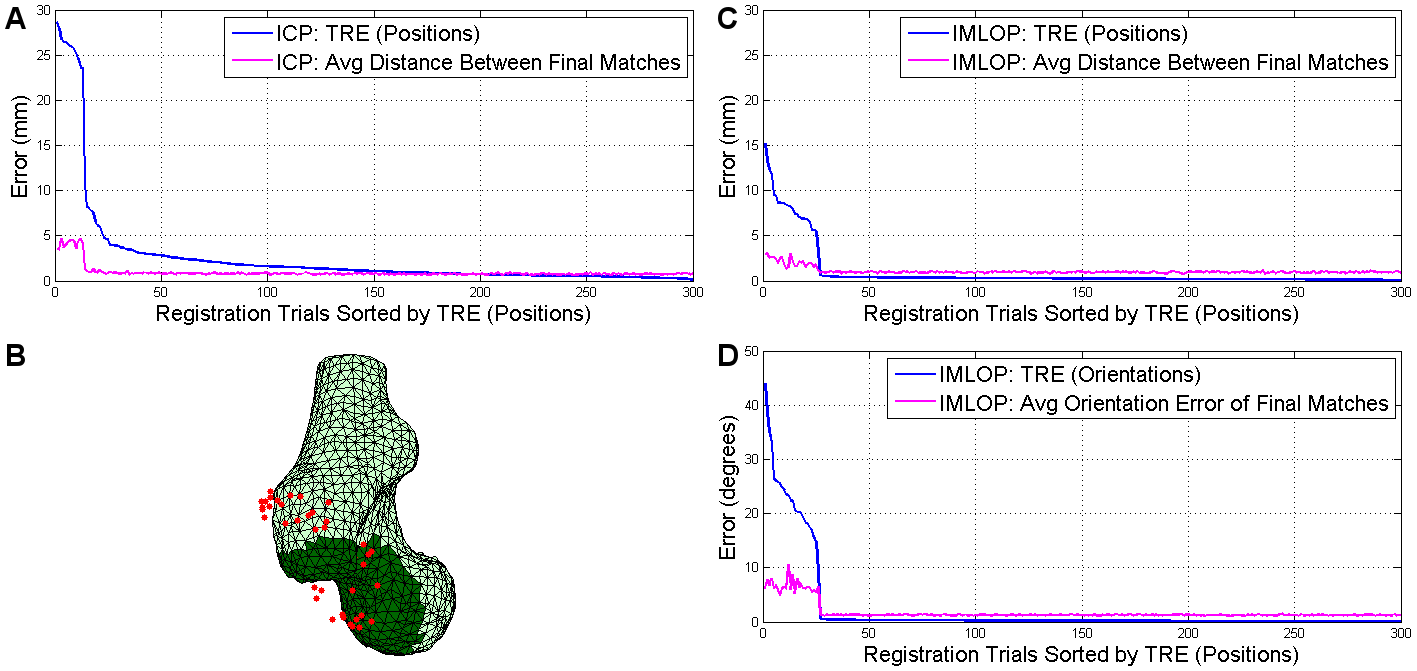
We introduce a new probabilistic variant of the ICP algorithm, namely Iterative Most Likely Oriented Point (IMLOP), which incorporates both surface position and surface normal information to compute an alignment of two shapes. A probabilistic framework is used to incorporate the position and orientation data into both the correspondence and registration phases of the algorithm, where orientation data is treated as Fisher distributed and position data is treated as Gaussian distributed. For the correspondence phase, we present a novel search algorithm that efficiently computes the most probable matches considering both position and orientation information of the target shape and of the source points being matched. For the registration phase, we present a closed-form solution to the problem of computing the rigid body transformation that maximizes the likelihood of the oriented point matches under the probabilistic noise model.

Experiments by simulation using human femur data segmented from CT imaging indicate that IMLOP is able to register shapes with a higher degree of accuracy than ICP. By evaluating the final residual error in both position and orientation of the final matches, IMLOP is able to automatically detect when a “correct” registration has been achieved. We demonstrate that IMLOP's criteria for detecting a registration failure is much more robust than what is possible using the sub-set of this criteria that is available to ICP. Finally, in our tests IMLOP computed a registration solution is less than half the run-time of ICP on average.

• Seth Billings
• Russell Taylor

• National Science Foundation, Graduate Research Fellowship Program (NSF GRFP)
• Johns Hopkins University Internal Funds

• Computer Integrated Interventional Systems Laboratory

• Seth Billings and Russell Taylor, Iterative Most Likely Oriented Point Registration, Accepted to MICCAI 2014

TODO following publication: The final publication is available at Springer via http://dx.doli.org/[insert DOI]