Table of Contents
Evaluation and Optimization of Virtual Rigid Body
Last updated: Date and time 05/09/2014
Summary
This project aims to develop experimental and analytical pipelines to design and evaluate optimal virtual rigid body configurations.
- Students: David Lee (dslee@cis.jhu.edu)
- Mentor(s): Alexis Cheng (acheng22@jhu), Dr. Emad M. Boctor (eboctor1@jhmi.edu)
 |  |  |
Background, Specific Aims, and Significance
In image-guided surgery, optical tracking system fulfills an important task of locating surgical tool in preoperative or intraoperative images for surgical operations. Optical tracking system largely consists of fiducial markers, which are rigidly attached to a tool to be tracked, and camera, which detects the fiducials. Detected positions of the rigid body fiducials serve to define a transformation from coordinate system of the camera to coordinate system of the tool. Using the transformation and some known, or calibrated, positions of the tooltip in tool coordinates, the tooltip can be identified in the camera space.
Several types of rigid body markers have been developed to provide accurate and convenient means of optical tracking. Active markers use sources such as LED to generate visible or infrared (IR) light; pseudo-passive markers have retro-reflective coating to reflect lights emitted from an external source; fully passive markers do not produce or reflect light and rely on visual patterns for detection. Fully passive markers, represented by a commercial system MicronTracker, have addressed problems in active and pseudo-passive markers associated with natural property of light, including quadratic decrease of intensity with increased marker-camera distance, and saturation when the markers are placed close to the camera.
Virtual rigid body is a novel type of marker that is tracked by an optical tracker. A projector is attached to a surgical tool, which projects markers of light onto the surface of interest. The markers are detected, and their positions in optical tracker coordinates are defined. Three of these markers are triangulated and fitted into a pyramidal model that uniquely characterizes the pose of the projector and the surgical tool. This project aims to evaluate and analyze the tracking accuracy of the virtual markers using different set of marker designs. The factors of interest include, but not limited to, size, shape, and number of the markers. These factors will be evaluated for sets of fixed or moving trajectory of the projector poses. From the analyses, the optimal design will be determined.
Deliverables
- Minimum: (03/31/2014) : COMPLETE
- Experimental Pipeline
- MicronTracker interface for virtual and physical fiducial detection.
- UR5 scripts for trajectory definition & pose recording
- Data processing routines
- VRB grid pattern
- Expected: (05/08/2014) : COMPLETE
- Data acquisition
- Analysis pipeline
- Error metric development
- VRB design: size, shape, number of lines
- Comparison between virtual and physical rigid body
- Basic optimal design of virtual markers
- Maximum: Aborted.
- Demonstration application to laparoscopy surgery – ABORTED
Technical Approach
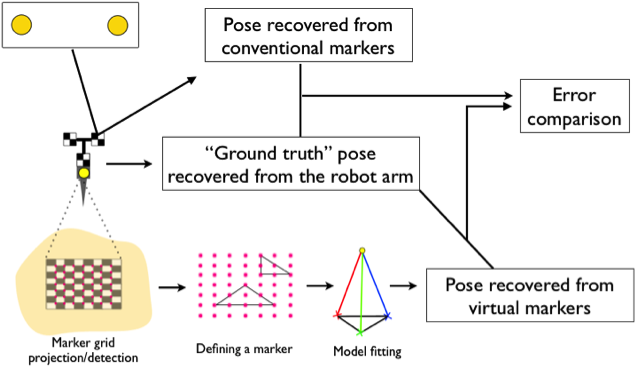 Performance of the virtual markers is evaluated by comparing the accuracy to that of the conventional markers. The projector is attached to a robot arm. A set of conventional markers is attached to the projector, while the projector shoots a grid (“checkerboard”) of virtual markers onto a surface of interest. A pose of the projector is recovered from the conventional markers. From the virtual marker grid, a set of three markers is selected to produce desired marker triangulation, and the pose is recovered. The recovered poses of the projector from conventional and virtual markers are compared with the ground truth pose extracted from the robot arm. This metric of accuracy is compared between the two types of markers.
Performance of the virtual markers is evaluated by comparing the accuracy to that of the conventional markers. The projector is attached to a robot arm. A set of conventional markers is attached to the projector, while the projector shoots a grid (“checkerboard”) of virtual markers onto a surface of interest. A pose of the projector is recovered from the conventional markers. From the virtual marker grid, a set of three markers is selected to produce desired marker triangulation, and the pose is recovered. The recovered poses of the projector from conventional and virtual markers are compared with the ground truth pose extracted from the robot arm. This metric of accuracy is compared between the two types of markers.
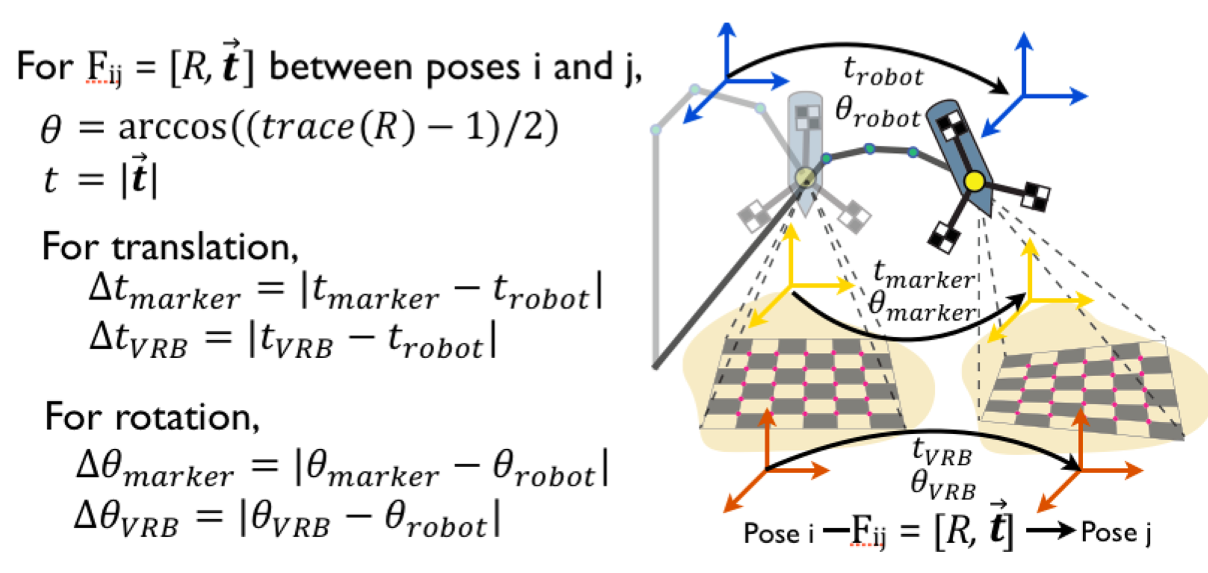
Error metric:
Dependencies
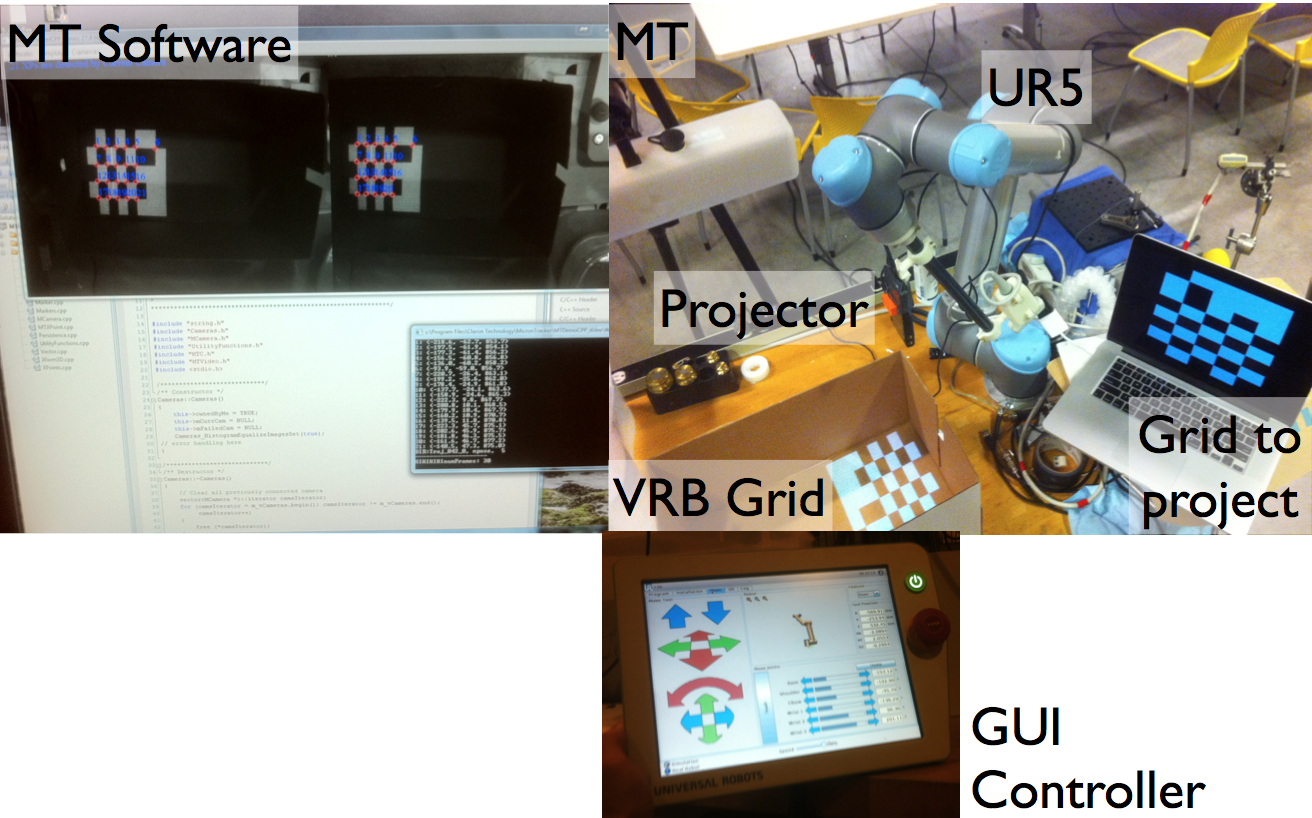
- Hardware
- MicronTracker (Optical tracker)
- Universal Robots robot arm and controller
- Robot - projector adapter (Broken and reprinted)
- Laptop
- Commercial Software
- MicronTracker SDK
- Universal Robots control system
- Internal algorithm and software
- Pose estimation of the projector given the coordinates of markers (Alexis)
- Error metric: Euclidean invariants (Alexis)
- Other software
- RANSAC plane fitting: found on web. Credits: Peter Kovesi, School of Computer Science & Software Engineering, The University of Western Australia
- Miscellaneous
- Access to Hackerman hall Robotorium
Milestones and Status
- Experimental Pipeline Setup
- Planned Date: 03/15/2014
- Completed Date: 03/15/2014
- Status: Marker grid defined, correspondence assigned, stable experimental setup complete.
- Experimental Design - Trajectory of motion and marker types
- Planned Date: 03/27/2014
- Completed Date: 03/24/2014
- Status: Pure translational and rotational motion / VRB design : size, shape, number of lines
- Experimental data
- Planned Date: 03/31/2014
- Completed Date: 05/05/2014
- Status: Repeatedly acquired new data. The “completed” data refers to the last data I took.
- Analysis Pipeline Setup
- Planned Date: 04/15/2014
- Completed Date: 04/22/2014
- Status: Basic pattern between VRB design and tracking accuracy identified.
- Evaluation and Analysis
- Planned Date: 04/15/2014
- Completed Date: 05/08/2014
- Status: Basic pattern between VRB design and tracking accuracy identified.
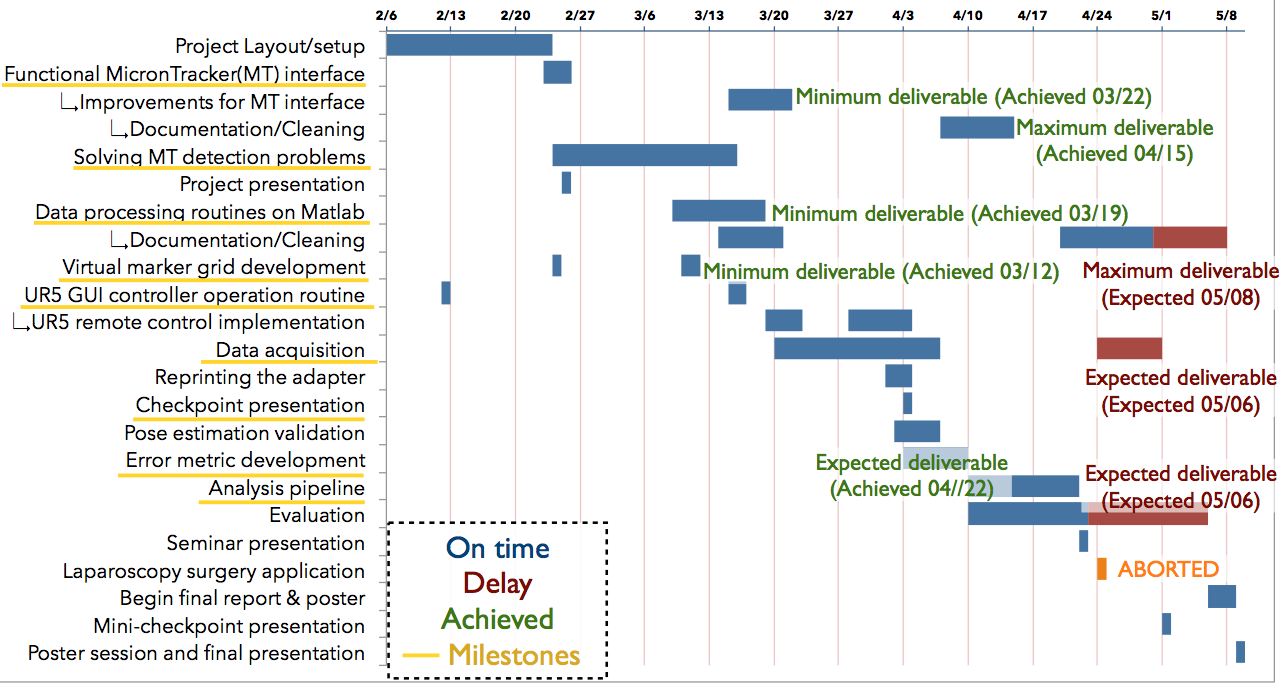
Reports and presentations
- Safety Certificate
- Project Plan
- Project Background Reading
- See Bibliography below for links.
- Project Checkpoint
- Paper Seminar Presentations
- Mini-checkpoint Presentation
- Project Final Presentation
- Project Final Report
Project Bibliography
- Cheng et. al., Virtual Rigid Body: A New Optical Tracking Paradigm in Image Guided Interventions, to appear in CARS 2014
- Mcllroy et. al., Kinectrack: Agile 6-DoF Tracking Using a Projected Dot Pattern, ISMAR, 2012
- West et. al., Designing Optically Tracked Instruments for Image-Guided Surgery, IEEE Transactions On Medical Imaging, 2004
- Wieness et. al., Sceptre - An Infrared Laser Tracking System for Virtual Environments, VRST, 2006
- Wiles et. al., Accuracy assessment and interpretation for optical tracking systems, Medical Imaging 2004: Visualization, Image-Guided Procedures, and Display, 2004
- Maier-Hein et. al., Comparative assessment of optical tracking systems for soft tissue navigation with fiducial needles, Medical Imaging 2008: Visualization, Image-guided Procedures, and Modeling, 2008
- Hummel et. al., Design and application of an assessment protocol for electromagnetic tracking systems, Med. Phys. 32, July 2005