Last updated: 05/09/19 10:30

The objective of this project is to develop and validate models for tool gravity compensation and arm deflection for the Galen Surgical System. The gravity compensation model will be implemented for multiple tools for static and dynamic cases.

• Students: Adam Polevoy, Parth Singh
• Mentor(s): Dr. Mahya Shahbazi, Dr. Russel Taylor

The Galen is a general purpose, hand-over-hand, admittance control robot developed mainly for otolaryngology. It is currently being commercialized by Galen Robotics inc, but was originally developed as PhD project in the LCSR and is still the subject of many research projects. The Galen reads values at a force/torque sensor and calculates the expected force/torque values at the user’s point of contact on a tool. The tool then moves proportionally to the force exerted, allowing a surgeon to use a tool with the additional benefits of stability and virtual fixtures. The force sensor, however, has no way distinguishing between the forces/torques exerted by the surgeon and those exerted by the tool itself. Currently the robot can cancel out values read at a particular moment, but rotating a tool results in new force/torque readings and often unintentional motion. The system also suffers from deflection issues, where the true position of the robot varies from the expected position because of flexibility in the joints.

Therefore, the objective of this project is to develop and validate models for gravity compensation and deflection for the Galen Surgical System. The gravity compensation model will be implemented for multiple tools and for static and dynamic motion.

• Minimum: (Completed)
  1. Report with data and analysis demonstrating a model capable of predicting 6 DoF forces and torque given a tool and tool holder pose due to gravity, along with code and documentation
  2. Video and data demonstrating successful integration of gravity compensation into robot control software, along with code and documentation

• Expected: (Partially Completed)
  1. Report demonstrating a model capable of predicting deflection forces at any point in the Galen workspace.
  2. C++ code and documentation of model that can be integrated with Galen code.

• Maximum: (Incomplete)
  1. Report demonstrating a model capable of predicting 6 DoF forces and torque given a tool and tool holder pose due to dynamic motion, along with code and documentation
  2. Video and data demonstrating successful integration of dynamic model compensation into robot control software, along with code and documentation

o

1) Static Compensation There are three models that our technical approach will employ, each increasingly complex. The first model is a simple static gravity compensation. The force and torque due to gravity can be represented as wrench vectors.

Ft is the wrench on the tool due to gravity and Fb is the wrench on the tool adaptor, as well as other non-tool components that could affect the force sensor, due to gravity. These are both in frames that are parallel to the base frame. The rotation matrix between the sensor and this global frame (the tool frame) can be calculated as:

Here, s is the sensor frame, b is the tool adaptor frame, and t is the tool frame. Rbs, for example, is the rotation from the b frame to the s frame. pbs is the translation from the b frame to the s frame. Rbs(0) denotes the rotation of the force sensor on the robot without any roll or tilt. Assuming that the force sensor is biased without any tool when there is no roll or tilt and when the tool is not attached, the wrench at the sensor, without any tool attached, can be calculated as:

Adg denotes the adjoint matrix of g. gbs denotes the transformation between frame b and frame s. Given enough data, the bias weight and center of mass of the tool adaptor can be estimated via a least squares method using the following equations:

Likewise, assuming the same bias condition, once a tool is attached, the wrench at the sensor can be calculated as:

Again, given enough data, the tool weight and tool center of mass can be estimated via a least squares method using the following equations. Then, this equation can then be used to predict the force sensor readings. The true readings minus the predicted readings would then be the compensated force sensor values.

An image of the robot with the mentioned wrench vectors is shown below

2) Dynamic Compensation Since the tool is ideally rigidly attached to the force sensor, there should be no dynamic components that need to be compensated. However, since there are some flexibilities in the system, this is most likely not the case. Therefore, currently, our plan is to fit a model from commanded velocities/angular velocities of the joints to the force sensor readings. This model will be selected after data collection has been completed.

Once these models have been developed, our gravity compensation system can be represented as a block diagram.

In order to model the deflection of the system, we will collect force sensor data, joint angles, tool position as reported by the robot, and tool position as measured by an optical tracker. (add deflection tech approach)

3) Deflection Characterization Lastly, we will build a model of arm deflection in the system due to forces and position applied to the tool at the robot end-effector. We will first create a CAD model for a tracker tool that can be attached to the new tool adaptor used on the Galen system. This will be 3D printed and tracker bodies will be attached.

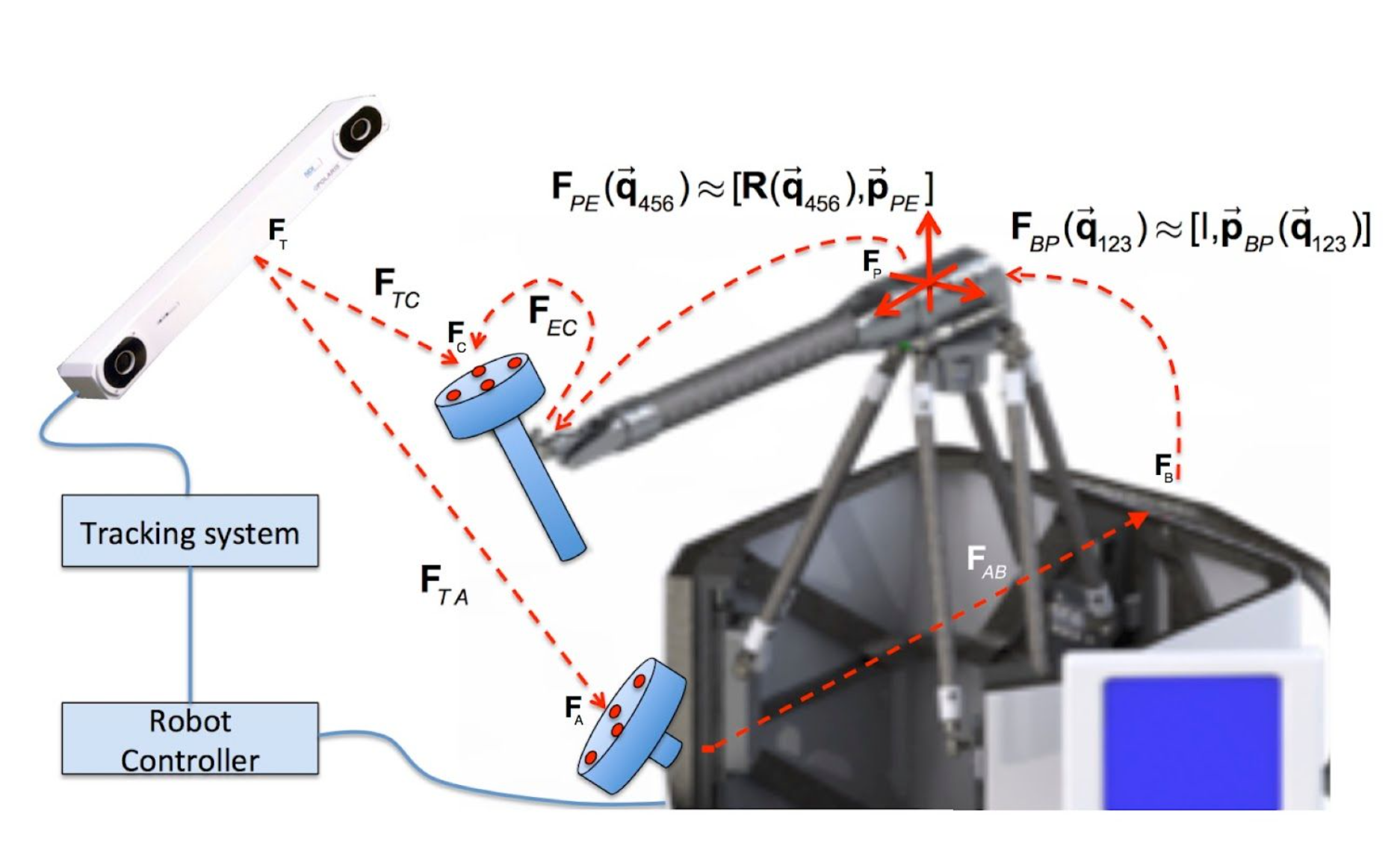Image Credit: CIS 1 2018 homework 4

We begin by finding the frame transformations shown in the image above. F BP and FP E for a given position can be calculated using the Galen forward kinematics. F EC is a static displacement that will be determined from the tracker tool CAD model and will be verified. F TC and F TA will be reported by the Optical Tracking System. F AB can be found by assuming no deflection at the home position with no force and calculating

We then move the robot to various positions within the workspace and apply forces in different directions, recording force sensor data, joint angles, tool position as reported by the robot, and tool position as measured by an optical tracker. We calculate the expected position using 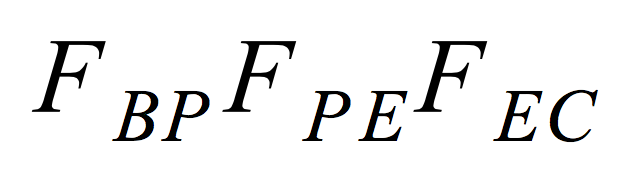and the actual position using .

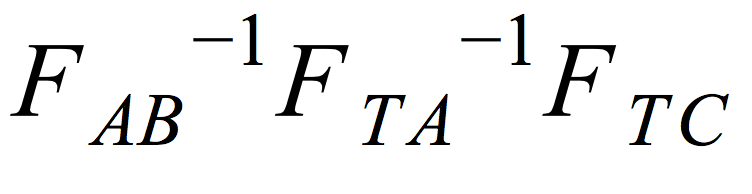After collecting this data and doing the calculations above, we will develop a model to predict the deflection values at a location using a shallow neural net. We will attempt different configurations and document the performance of each. Parameters that we will change will include the number of layers, activation function, and loss function.

• Access to MockOR
  • Solution: Fill out paperwork
  • Alternative: N/A
  • Date: N/A
  • Status: Resolved
• Access to Galen Mark 1
  • Solution: Speak with Galen Commercial team about scheduling
  • Alternative: Use Galen Mark 0
  • Date: 2/14
  • Status: Resolved
• Access to Galen Bitbucket Repository
  • Solution: Email Barry Voorhees
  • Alternative: Speak to Galen Team/Dr. Taylor. Worst Case, use old LCSR repo and mark 1
  • Date: 2/14
  • Status: Resolved
• Get access or knowledge about previously used data collection on the Galen
  • Solution: Email Paul Wilkening
  • Alternative: Read through code and write our own script.
  • Date: 2/14
  • Status: Resolved
• Discuss tool exchange
  • Solution: Speak with Dave Levi
  • Alternative: Use Galen Mark 1
  • Date: 2/14
  • Status: Resolved
• Login Access to Galen Computers
  • Solution: Resolved
  • Alternative: N/A
  • Date: N/A
  • Status: Resolved
• Access to atracsys optical tracker
  • Solution: Email Dr. Taylor
  • Alternative: Ask Dr. Taylor about alternative optical trackers
  • Date: 4/1
  • Status: resolved
• Access to 3d printer for tracker tool
  • Solution: Speak with Dave Levi about LCSR printer
  • Alternative: Speak with Dr. Taylor about funds for Wyman printer
  • Date: 4/1
  • Status: resolved
• Access to tracker bodies
  • Solution: Speak with Galen Team
  • Alternative: Use Micron tracker and print out trackers
  • Date: 4/1
  • Status: resolved

1. Functional Data Collection Script:
   • Planned Date: 02/22/19
   • Expected Date: 02/22/19
   • Status: Completed
2. Functional Static Prediction Model:
   • Planned Date: 03/04/19
   • Expected Date: 03/04/19
   • Status: Completed
3. Integrated Static Compensation:
   • Planned Date: 04/04/19
   • Expected Date: 04/04/19
   • Status: Completed
4. Deflection Data Collected:
   • Planned Date: 04/24/19
   • Expected Date: 04/24/19
   • Status: Completed
5. Functional Deflection Model:
   • Planned Date: 05/04/19
   • Expected Date: 05/04/19
   • Status: Partially Completed
6. Functional Dynamic Prediction Model:
   • Planned Date: 04/24/19
   • Expected Date: 04/24/19
   • Status: Not Completed
7. Dynamic Compensation Integrated:
   • Planned Date: 05/01/19
   • Expected Date: 05/01/19
   • Status: Not Completed
8. Final Report/Presentation:
   • Planned Date: 05/16/19
   • Expected Date: 05/16/19
   • Status: Completed

• Project Plan
  • gravity_compensation_project_plan_proposal.pdf
  • proposal_v4.pdf
• Project Background Reading
  • See Bibliography below for links.
• Project Checkpoint
  • group_4_project_checkpoint_presentation.pdf
• Paper Seminar Presentations and Critical Reviews
  • adam_seminar_presentation.pdf
  • critical_review.pdf
  • parth_seminar_presentation.pdf
  • parth_paper_critique.pdf
• Project Final Presentation
  • group4poster_ms_may07-2019.pdf
• Project Final Report
  • cis2_group4.pdf
  • links to any appendices or other material

• Beer, Randall F., et al. “Development and evaluation of a gravity compensated training environment for robotic rehabilitation of post-stroke reaching.” Proc. 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob). 2008.
• D. A. Fresonke, E. Hernandez and D. Tesar, “Deflection prediction for serial manipulators,” Proceedings. 1988 IEEE International Conference on Robotics and Automation , Philadelphia, PA, USA, 1988, pp. 482-487 vol.1.
• Dimeas, Fotios & Aspragathos, Nikos. (2015). Learning optimal variable admittance control for rotational motion in human-robot co-manipulation. IFAC-PapersOnLine. 48. 10.1016/j.ifacol.2015.12.021.
• Feng, Allen L., et al. “The robotic ENT microsurgery system: A novel robotic platform for microvascular surgery.” The Laryngoscope 127.11 (2017): 2495-2500.
• Kim, Woo Young & Han, Sanghoon & Park, Sukho & Park, Jong-Oh & Ko, Seong Young. (2013). Tool Gravity Compensation for Maneuverability Enhancement of Interactive Robot Control for Bone Fracture Reduction System.
• Lehmann , Tavakoli, Usmani, and Sloboda, “Force-Sensor-Based Estimation of Needle Tip Deflection in Brachytherapy,” Journal of Sensors , vol. 2013, Article ID 263153, 10 pages, 2013.
• Luo, Ren C., Y. Yi Chun, and Yi W. Perng. “Gravity compensation and compliance based force control for auxiliarily easiness in manipulating robot arm.” Control Conference (ASCC), 2011 8th Asian. IEEE, 2011.
• Olds, Kevin. Robotic Assistant Systems for Otolaryngology-Head and Neck Surgery. Diss. 2015.

Here give list of other project files (e.g., source code) associated with the project. If these are online give a link to an appropriate external repository or to uploaded media files under this name space (2019-04).