Contact Us
CiiS Lab
Johns Hopkins University
112 Hackerman Hall
3400 N. Charles Street
Baltimore, MD 21218
Directions
Lab Director
Russell Taylor
127 Hackerman Hall
rht@jhu.edu
Last updated: 3/23/2021 1900
Our goal is to improve the usability of tubular retractors in deep lesion brain surgery. One of the largest considerations in these procedures is minimizing cortical disruption and the associated brain trauma. Currently, retractors need to be repositioned by hand, which is a tedious process that introduces excess noise. We propose a new system to reposition these retractors using motorized control to increase the accuracy and precision of the process.
Current methods for neurosurgical retraction are well-documented for imparting excessive focal pressure on the brain, leading to high risk of injury. Of the 700,000 neurosurgical cases each year in the US requiring brain retraction, about 9%, or 63,000 cases, exhibit acute retraction-induced injury. Given that major complications cost roughly $50,000 for the patient and that each day spent in the hospital costs around $2,500, this amounts to a $3 billion burden on the US healthcare system due to retraction-induced injury.
A case study series where surgeons compared the NICO BrainPath retractor to conventional metal blade retractors found a 50% reduction in length of stay, and this reduced ICU time saved critical care facilities $17,000 in direct variable costs on average per retractor use2. Developing a safer alternative to typical manual use of tubular retractors such as the BrainPath can protect the health of patients undergoing difficult, relevant surgeries, and reduce the associated financial load on hospitals. This project will improve the safety by decreasing potential unregulated or high-noise movements that are derived from human error during manual adjustments of the retractor. Operational effectiveness will also be increased through more operable controls done through autonomous retractor adjustment to state of surgical procedure.
This project aims to stabilize a custom tubular retractor by attaching it to a flexible snake arm and add the capability to electronically adjust tubular retractor orientation during use. Our second goal is to improve usability further by adjusting the distal end of the retractor to follow the tip of the surgical tools in use. The final project goal is to allow alignment of the view through the distal end of the retractor with the surgical microscope’s field of vision. This project endeavors to create the first mechatronic application of tubular retraction, and in doing so, improve surgical experience and outcome by improving device usability and safety.
The intermediate component (Fig. 6) will provide a secure connection between a surgical snake arm and a tubular retractor, fit into the circular cranial aperture fenestrated during the surgical craniotomy, and concurrently bypass the profile of the skull, which is high relative to the sunken brain. The snake arm will remain rigidly in a position dictated by the surgeon during the procedure, as seen in the current standard of care devices; thus, we will implement this aim with the use of market-available snake arms, such as the Leyla Retractor arm. The connecting component will take on the form of a metallic ring in order to fit inside the circular skull hole.
Figure 6: Mechanical. The connecting component (dark grey) is attached to the tubular retractor and the snake arm (black). The control pad (blue) is at the base of the retractor.
Figure 7: CIS goal. The tubular retractor rotates for angulation about the base motor and the axle on the connecting component (both yellow). Wires that are responsible for rotating the spindle are not shown.
Figure 8: First prototype. This gives us 2 degrees of freedom with an upscaled 2-axis gimbal structure. Next steps for this include making it more compact to fit into surgical work area.
Our first implementation of the mechanical design uses servos for actuation and a 2-axis gimbal structure to give the fixture 2 degrees of freedom, seen in the above figure. Implemented methods of control include through use of buttons for more predictable incremental control for the surgeon, a joystick for an intuitive control that uses hand-eye coordination, synchronized control using our calibration object, and some progress on manual control with velocity limiting features through PD control.
Demonstration: Button Control Demonstration: Joystick Control
Because the ring mention in the project goal, shown in greater detail in Fig. 8, will require actuation, the attachment will have a built-in axle (a) to which the retractor will attach. While the retractor will attach to the narrow section of the axle seen on the side of component a1, the forces causing rotation will be applied by thin strings connected to the widened section of the axle seen in component a2. The motor responsible for this rotation will be located somewhere at the base of the device (not shown). The strings will stretch from the axle shaft (a2) to this motor through the transmission housing (e). The axle (a2) will be inserted through a small hole and closed up by the spring plug (b). This is necessary so that the surgeon can press in on the axle, load the retractor, and, upon release, firmly secure the retractor in place. The rotation about the other axis will be performed by a motor or axle sitting in component f. Component c will help support this structure by providing a track along which the outer rings of the motor housing (f) will spin. The attachment will avoid obstruction by the skull due to a narrow extension that will protrude upwards from the ring attachment. This extension will interface with the snake arm through coupling this component to a local connector (d) that will screw into the tip of the snake arm in use. This system will be able to be connected in between the snake arm and retractor after the retractor has already been inserted into the brain.
Figure 9: Mechanical Design CAD. The retractor will be inserted into the ring, with which its circular cross-section will be concentric.
Retractor angulation will require the retractor to be capable of control by surgeon interaction in fine rotational steps about two horizontal axes (Fig. 7). The surgeon will be able to press buttons on a directional pad or joystick style controller to control two sets of motors, each set responsible for rotating about one horizontal axis. This first set will consist of one micromotor that will be part of the local connector screwed into the tip of the snake arm. The second set will consist of two micromotors, enclosed at the base of the Leyla arm, that, when synchronized, will provide clockwise and counterclockwise motion, through wires that extend along the system, to the axle that will lodge into the retractor. These wires will be directed along a minimally obtrusive trajectory with the help of low-friction internal mechanical geometry. If we discover that this design is not optimal, we may explore other designs. One possible design is a “turret rotation” mechanism which will rotate the outer ring about its central axis. The angling will be done by tilting the central axis with respect to the vertical. This will be accomplished through a motor sitting on top of the ring. This design is anticipated to be less effective because the motor may obstruct the path of surgical instruments. To fine tune the design or select another, “two-axis gimbal” structures will be researched.
The motorized alignment of the retractor will utilize the developed actuation method to realign the tubular retractor’s scope of vision, such that its angle of orientation matches that of the surgeon’s surgical forceps, upon surgeon command (i.e. a button or foot pedal). The surgical forceps will be fitted with 9 DoF inertial measurement units (IMUs) that will be constantly collecting tri-axial magnetometer, gyroscope, and accelerometer readings. This data will then be fused to create orientation estimates (for now, this will be in the form of Euler angles) using an Orientation Estimation algorithm. For now, we plan to use either the Madgwick Filter (described in this paper: Madgwick Paper) or the Mahony Filter (described in this paper: Mahony Paper. The choice will depend on the accuracy of the experimental results we obtain from both static and dynamic testing. Note that we used the implementations of these filters from the Arduino library Adafruit AHRS.
Both of these algorithms (in the case of a 9 DoF IMU), fuse the data from the three main sensors on our IMU to remove drift, a common problem with cheap sensors such as IMUs.
The initial results using the Madgwick Filter appear quite promising with respect to drift. Shown below is the average degree deviation (Zero-centered) in X, Y, and Z over time when the sensor is kept constant. As noted before, we are currently using Euler angles to represent our orientation so X, Y, and Z can take values in the range of [-180 degrees, 180 degrees]. For the following results, we kept the sensor still for a period of 5 minutes without touching it at all, and allowed the Madgwick filter to calculate the orientation throughout the experiment. We then repeated this for a total of 11 trials. We repeated this entire procedure two more times for different resting orientations (i.e. the sensor facing different directions to see which is best). Shown below are the average results of the trials with the sensor laying flat on the table (i.e. the sensor's z-axis facing up - please note the sensor's axes don't necessarily match up with the orientation axes, but in this one orientation they do).
Please note that the first 580 (~1 min) samples have been removed for analysis as we see issues with start-up that subside at this time.
Once, we have finalized our orientation estimation algorithm, we will place these 9 DoF IMUs on both the tubular retractor and the calibration object/forceps so that both objects orientations are being constantly measured. We will then have to perform some sort of registration which has yet to be determined so that the orientations are in the same coordinate system. Once that is done, then, upon the press of a button by the surgeon, the motors holding the retractor will slowly move the retractor so that its orientation matches the orientation of the forceps at the time the button was pressed. This movement will be done very slowly so as to not create any unnecessary force on the brain tissue.
For the robot movement, we plan to be able to move with a resolution of 1 degree using a step motor that has its steps split up to an even finer resolution (see mechanical approach for more details). Moreover, we plan to be able to move within a range of approximately 15 degrees during a procedure as this was described as a hard maximum by one of our clinical advisors.
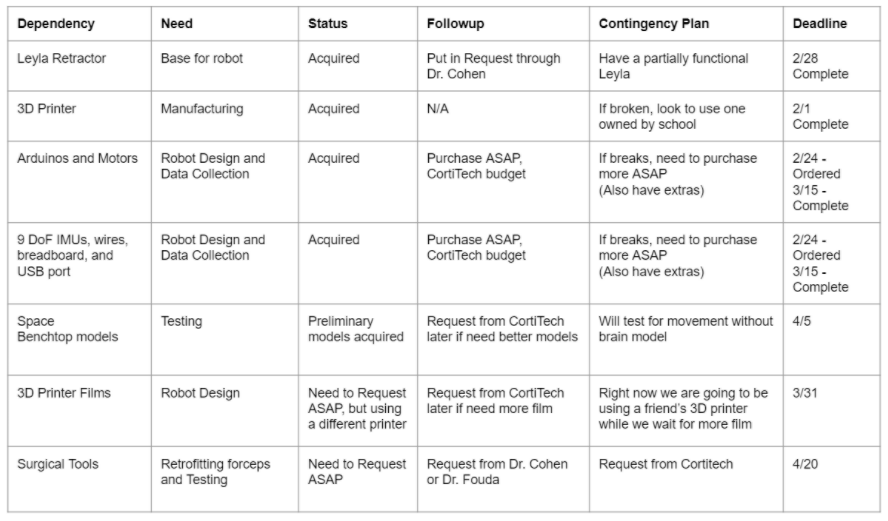
Here give list of other project files (e.g., source code) associated with the project. If these are online give a link to an appropriate external repository or to uploaded media files under this name space (2021-01).
